Partitioning

Overview

The largest LSST tables will not fit on a single node in the projected production time-frame, and so must be partitioned into smaller pieces and spread over many nodes. Qserv uses a spatial partitioning scheme. A dominant table is chosen containing sky coordinates that are used for partitioning; for LSST data releases, this is the Object table. All other tables that contain a foreign key into the Object table are partitioned by the position of the associated Object, or by a fall-back position if an associated Object is not guaranteed to have been assigned. This means for example that all the single-exposure sources associated with a particular Object will end up in the same partition, even if that Object has non-trivial proper motion. Large tables (e.g. catalogs from other surveys) that are not directly related to Object are also partitioned by position, using the same scheme and parameters. This results in perfectly aligned partition boundaries, simplifying the implementation of near-neighbor joins. The following excerpt from Qserv: A distributed shared-nothing database for the LSST catalog further describes some of the motivations for partitioning data in Qserv:

Qserv divides data into spatial partitions of roughly the same area. Since objects occur at a similar density (within an order of magnitude) throughout the celestial sphere, equal-area partitions should evenly spread a load that is uniformly distributed over the sky. If partitions are small with respect to higher-density areas and spread over computational resources in a non-area-based scheme, density-differential-induced skew will be spread among multiple nodes.

Determining the size and number of data partitions may not be obvious. Queries are fragmented according to partitions so an increasing number of partitions increases the number of physical queries to be dispatched, managed, and aggregated. Thus a greater number of partitions increases the potential for parallelism but also increases the overhead. For a data-intensive and bandwidth-limited query, a parallelization width close to the number of disk spindles should minimize seeks while maximizing bandwidth and performance.

From a management perspective, more partitions facilitate re-balancing data among nodes when nodes are added or removed. If the number of partitions were equal to the number of nodes, then the addition of a new node would require the data to be re-partitioned. On the other hand, if there were many more partitions than nodes, then a set of partitions could be assigned to the new node without re-computing partition boundaries.

Smaller and more numerous partitions benefit spatial joins. In an astronomical context, we are interested in objects near other objects, and thus a full O(n^2) join is not required — a localized spatial join is more appropriate. With spatial data split into smaller partitions, a SQL engine computing the join need not even consider (and reject) all possible pairs of objects, merely all the pairs within a region. Thus a task that is naively O(n^2) becomes O(kn) where k is the number of objects in a partition.

In consideration of these trade-offs, two-level partitioning seems to be a conceptually simple way to blend the advantages of both extremes. Queries can be fragmented in terms of coarse partitions (“chunks”), and spatial near-neighbor joins can be executed over more fine partitions (“subchunks”) within each partition. To avoid the overhead of the subchunks for non-join queries, the system can store chunks and generate subchunks on-demand for spatial join queries. On-the-fly generation for joins is cost-effective due to the drastic reduction of pairs, which is true as long as there are many subchunks for each chunk.

Note that if each point is assigned to exactly one partition, then a spatial join cannot operate on a single partition at a time because two nearby points could belong to different partitions. Dealing with outside partitions requires data exchange, complicating the Qserv implementation. To avoid this, Qserv stores a precomputed amount of overlapping data along with each partition.

The Partitioning Scheme

The celestial sphere is divided into latitude angle “stripes” of fixed height H. For each stripe, a width W is computed such that any two points in the stripe with longitude angles separated by at least W have angular separation of at least H. The stripe is then broken into an integral number of chunks of width at least W. The same procedure is used to obtain finer subchunks - each stripe is broken into a configureable number of equal-height “substripes”, and each substripe is broken into equal-width subchunks. This scheme was chosen over e.g. the Hierarchical Triangular Mesh for its speed (no trigonometry is required to locate the partition of a point given in spherical coordinates), simplicity of implementation, and the fine control it offers over the area of chunks and sub-chunks.

Partition Identifiers

Partition identifiers are integers. No assumptions about the properties of these IDs (e.g. consecutiveness, non-negativity, etc… ) should be made outside of the partitioning code itself. For the record, here is how these identifiers are currently assigned.

First, stripes are numbered from 0 to S - 1, where 0 denotes the southernmost stripe. Within a stripe s, chunks are numbered from 0 to C_s - 1, where 0 denotes the chunk with minimum longitude = 0. Note that according to the rules above, 2S >= C_s for any s. The identifier (chunk ID) for chunk c in stripe s is given by:

2S*s + c

Similarly, the identifier (subchunk ID) for subchunk c in substripe s within a particular chunk is:

M*s + c

where M is the maximum number of sub-chunks that fit in a single sub-stripe of any chunk.

Overlap

The boundaries of chunks and subchunks constructed as described are boxes in longitude and latitude angle. It is relatively straightforward to compute a spherical box that is a conservative approximation to the region containing all points within angular separation R of an initial box - the latitude limits must be adjusted outwards by R, and longitude bounds for the shape obtained by sweeping a small circle of opening angle R along the sides of the box must be computed.

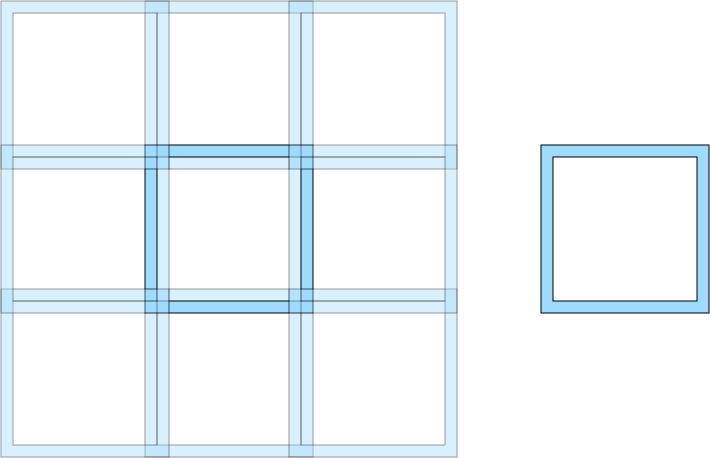
In the image above, the white square on the right is a subchunk. The overlap region of this subchunk consists of the light blue region around it. On the left, a tiling of multiple subchunks is shown.

Qserv implements a spatial join that finds objects in two distinct tables U and V separated by an angle of at most R by taking the union of the following over all subchunks:

(
    SELECT ...
    FROM U_p, V_p
    WHERE scisql_angSep(U_p.ra, U_p.decl, V_p.ra, V_p.decl) <= R AND ...
) UNION ALL (
    SELECT ...
    FROM U_p, OV_p
    WHERE scisql_angSep(U_p.ra, U_p.decl, V_p.ra, V_p.decl) <= R AND ...
)

Here, U_p and V_p correspond to the subchunk p of U and V (which must be identically partitioned), and OV_p contains the points inside the overlap region of p.

Match Tables

Match tables store a precomputed many-to-many relationship between two identically partitioned tables U and V. For example, a match table might store a mapping between reference objects and objects that facilitates data production QA.

A row in a match table M consists of (at least) a pair of foreign keys into the two related tables. A match in M is assigned to a subchunk P if either of the referenced positions to is assigned to P. If no positions in a match are separated by more than the overlap radius, then a 3-way equi-join between U, M and V can be decomposed into the union of 3-way joins over the set of subchunks P:

(
    SELECT ...
    FROM U_p INNER JOIN M_c ON (U_p.pk = M_c.fk_u)
             INNER JOIN V_p ON (M_c.fk_v = V_p.pk)
    WHERE ...
) UNION ALL (
    SELECT ...
    FROM U_p INNER JOIN M_c ON (U_p.pk = M_c.fk_u)
             INNER JOIN OV_p ON (M_c.fk_v = OV_p.pk)
    WHERE ...
)

U_p and V_p correspond to the subchunk p of chunk c of tables U and V. M_c corresponds to chunk c of table M, and OV_p is the subset of V containing points in the full overlap region of subchunk p. Note that queries which involve only the match table need to be rewritten to discard duplicates, since a match pair linking positions in two different chunks will be stored twice (once in each chunk).

Object movement

The fact all tables will be partitioned according to Object RA/Dec implies that in rare cases when an object is close to the partition edge, some of its sources may end up in a partition that is different from the “natural” one for the source’s own ra/dec. To address this issue, the Qserv master will expand the search region by an distance R when determining which partitions to query, where R is large enough to capture object motion for the duration of the LSST survey to date. The WHERE clause applied by Qserv workers to their Source table partitions will use the original search region to ensure that the query semantics are preserved. Without this, some sources inside the search region assigned to objects outside the search region and that lie across partition boundaries might be missed.